В данной статье речь пойдѐт, главным образом, о полосовых фильтрах промежуточной частоты 455 и 465кГц. Название «дискретные» означает то, что они составлены из отдельных пьезокерамических элементов, называемых резонаторами. В начале ХХ века, когда был изобретѐн супергетеродинный приѐмник, радиотехники выбрали для неготакие промежуточные частоты, отнюдь не имея в виду перспективу осуществления селекции фильтрами на пьезокерамике.
Однако именно такие частоты, 400 – 500кГц, оказались как нельзя более подходящими для пьезокерамических фильтров. Именно такие частоты способствовали созданию дешёвых, технологичных фильтров, и их размеры оказались в десятки раз меньше, чем у фильтров сосредоточенной селекции на катушках и конденсаторах. Пьезокерамические резонаторы, из которых строится фильтр, обычно выполняют в форме диска диаметром 5 – 6 мм или квадрата со стороной около 5мм. Характеристики фильтра всецело зависят от параметров и количества резонаторов их составляющих.
Далее попытаемся дать представление о том, как работает дискретный полосовой пьезокерамический фильтр и о том, как конструктивно устроены фильтры, выпускаемые в промышленных масштабах. При этом несколько пожертвуем научной строгостью, опустив подробности, которые не столь существенны для первого знакомства. Для начала разберёмся с резонаторами, элементарными кирпичиками фильтров.
Пьезокерамические резонаторы
Чем отличается пьезорезонатор от пьезоэлемента? Пьезорезонатор это «улучшенный» пьезоэлемент, если его рассматривать с позиции применения, то есть как колебательный элемент. Резонансная частота резонатора, для выбранного типа колебаний, должна возможно дальше отстоять от частот других типов колебаний. Это достигается конструктивно, путём выбора частотоопределяющего размера, по возможности, значительно больше или меньше других. Резонатор должен обладать достаточно высоким значением механической добротности и высокой стабильностью частоты во времени и в интервале рабочих температур. Это достигается путём выбора подходящей марки пьезокерамического материала. В фильтрах, являющихся предметом нашего рассмотрения, используются дисковые резонаторы, где в качестве основного типа колебаний используются радиальные колебания. Частота радиальных колебаний зависит от радиуса и не зависит от толщины. При таких колебаниях центр диска остаётся неподвижным, и это позволяет, не возмущая процесс колебаний, осуществить электрический и механический контакт в этой неподвижной точке.
Теперь посмотрим на поведение пьезокерамического резонатора. От чего зависит его резонансная частота? Во-первых, от диаметра. Чем больше диаметр, тем ниже частота. Произведение диаметра на частоту – величина постоянная. Она называется частотной постоянной. При заданной длине диаметра резонансная частота определяется всего двумя характеристиками материала из которого он изготовлен. Это плотность и упругость. Как возбудить радиальные колебания диска? Очень просто. Надо приложить переменное усилие по толщине диска. Деформируя диск по толщине, мы вызываем ответную деформацию в перпендикулярном направлении. Это происходит потому, что любое твёрдое тело стремится сохранить свой объём. Разным телам это удаётся по-разному, но в среднем деформация в поперечном направлении составляет 1/3 от деформации в направлении приложенной силы. Так как материал резонатора является пьезоэлектриком, то вынуждающую силу можно создать за счёт пьезоэффекта. Таким образом, приложив переменное напряжение вдоль толщины, можно возбудить радиальные колебания, в том числе, на резонансной частоте.
Далее попытаемся удивить читателя следующим экспериментом. Будем возбуждать в резонаторе свободные затухающие колебания, действуя одиночными импульсами достаточно высокого напряжения длительностью, примерно, полпериода резонансной частоты радиальных колебаний. На рис. 1а такой импульс подаём путём размыкания и замыкания ключа, а на рис.1б, наоборот, путём замыкания и, через полпериода, размыкания ключа.
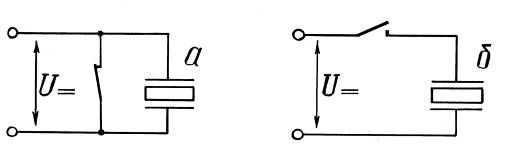
Рис.1. Возбуждение пьезокерамического резонатора путём кратковременного размыкания ключа (а) и кратко-временного замыкания ключа (б).
Такое ударное воздействие возбуждает в резонаторе свободные колебания, частоту которых, без особых технических проблем, можно измерить. Оказывается, частоты свободных колебаний разные! Отличие достигает 20%. Всё дело в условиях, в которых наблюдаем колебательный процесс. В первом случае наблюдаем колебания резонатора с закороченными электродами, а во втором – с разомкнутыми. В первом случае потенциал электродов равен 0 (в общем случае – постоянный), тогда как во втором случае, вследствие пьезоэффекта, переменный. Знак изменяющегося напряжения между электродами всегда таков, что оно всегда, как и сила упругости, старается вернуть колеблющийся элемент к положению равновесия. То есть, возникающее вследствие пьезоэффекта напряжение «помогает» силе упругости. Сила упругости или, иными словами, жёсткость становится больше, а значит частота выше. Чем эффективнее пьезоэлектрик, тем больше «пьезодовесок» к силе упругости.
Рассмотрим поведение резонатора под действием вынуждающей силы синусоидальной формы. Соберём схему согласно рис.2 и будем наблюдать осциллограммы напряжений на резонаторе.
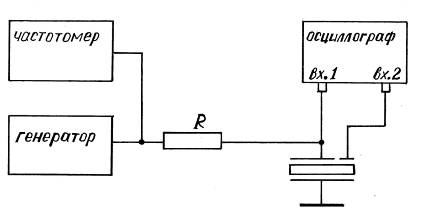
Рис.2. Схема возбуждения резонатора напряжением синусоидальной формы.
Резонатор в этой схеме не совсем обычен. На одном из его электродов «выцарапан» маленький контрольный электрод. Он нам нужен для того, чтобы следить за фактическим состоянием механического колебательного цикла. Ведь напряжение на контрольном электроде, который изолирован от основного, в точности воспроизводит деформацию резонатора. Напряжения с основного и контрольного электрода подадим на входы двухлучевого осциллографа. Настроив генератор на ту частоту, которую мы измерили в предыдущем опыте по рис.1а, заметим, что напряжение на резонаторе уменьшилось в десятки раз, а фазовый сдвиг между напряжениями на основном и контрольном электродах составил почти 180о (смотреть осциллограмму на рис.3 слева). Это означает следующее.
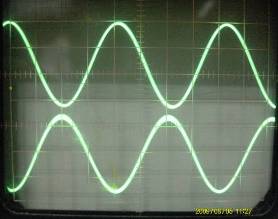
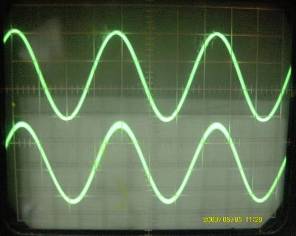
Рис.3. Осциллограммы напряжений на основном (вверху) и контрольном (внизу) электродах
Изменение заряда на основном электроде при механическом колебательном движении постоянно компенсируется притоком или оттоком зарядов от генератора. В результате потенциал остаётся, практически, постоянен и, тем самым, реализуется тот же режим, как с закороченными электродами, что на рис.1а. На контрольном же электроде такой компенсации не происходит и напряжение на нём остаётся близким к напряжению генератора. По существу мы убедились в том, что на данной частоте резонатор резко уменьшил своё сопротивление, а напряжение генератора перераспределилось на добавочный резистор R. Тот факт, что нам всё-таки удалось наблюдать осциллограмму, разумеется, при увеличенной чувствительности, свидетельствует о том, что резонатор обладает небольшим эквивалентным сопротивлением, связанным с тепловыми потерями в материале резонатора вследствие внутреннего трения.
На правом фотоснимке, на рис.3, представлена осциллограмма, когда, увеличивая частоту генератора, достигли максимального напряжения на основном электроде. Видим, что при этом фазовый сдвиг с напряжением на контрольном электроде стал близким к нулю. Вспомним, что контрольный электрод у нас изолирован, как и на рис.1б. Следовательно, также и основной электрод ведёт себя как изолированный. Генератор пытается дать заряды или снять заряды с резонатора, а резонатор их либо не берёт, либо не возвращает, либо «догоняет», либо «убегает». Он «выбрал» на этой частоте такую фазу механических колебаний, будто его электроды изолированы от внешнего мира, как контрольный электрод, как электроды на рис.1б. На этой частоте ток минимален, сопротивление велико. Некоторая проводимость резонатора опять же связана с тепловыми потерями в его теле. Потребляемая мощность идёт только на компенсацию этих потерь, она поддерживает незатухающие колебания. Разница в частотах также видна на осциллограммах.
Характерные частоты для двух рассмотренных картин, по принятой терминологии, называются резонансной fри антирезонансной fа частотой. Разность этих частот называют резонансным промежутком Δf. На частотах ниже резонансной и выше антирезонансной резонатор проявляет себя как конденсатор, ёмкость которого, главным образом, определяется площадью электродного покрытия и толщиной керамического диэлектрика, который имеет диэлектрическую проницаемость порядка 1000.
Каков порядок величин ёмкостного и эквивалентных активных сопротивлений резонаторов, применяемых в пьезокерамических фильтрах? Ёмкостное сопротивление имеет порядок 2-3 кОм. На резонансной частоте эквивалентное сопротивление имеет активный характер и порядок величины, в среднем, 50-100 Ом. На антирезонансной частоте его сопротивление также активно и имеет порядок сотен килоом. Величина ёмкостного сопротивления обычно равна среднему геометрическому сопротивлений на резонансе и антирезонансе. То есть, при настройке в резонанс сопротивление резонатора уменьшается во столько же раз, во сколько раз увеличивается сопротивление на антирезонансе.
Изучив поведение резонаторов в интервале частот, можно приступить к построению полосовых пьезокерамических фильтров.
Лестничная схема
Пьезокерамические фильтры, выпускаемые промышленностью, обычно выполняют по лестничной схеме. Эта схема позволяет наиболее просто и дёшево реализовать себя в конструктивном исполнении. Лестничный фильтр состоит из звеньев или ступеней. Простейший фильтр – однозвенный, а два последовательно соединённых резонатора представляют простейшее звено. На рис.4 показана схема двухзвенного лестничного фильтра, из которого становится ясным происхождение названия.
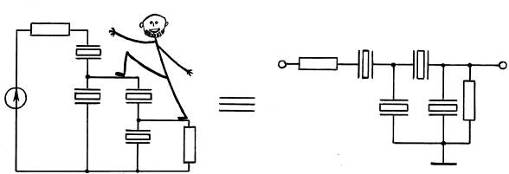
Рис.4. Принципиальные схемы двухзвенного лестничного фильтра.
На правой картинке изображена та же схема в общепринятом виде. Чтобы понять, как работает сколь угодно сложный фильтр, достаточно разобраться с работой отдельного звена.
Как фильтр фильтрует
|
|
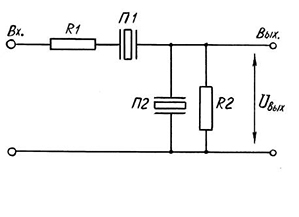
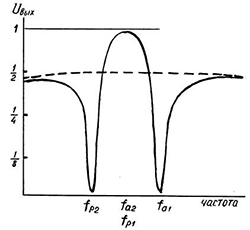
| Рис.5. Схема простейшего фильтра | Рис.6. Частотная зависимость выходного напряжения |
Рассмотрим схему простейшего, однозвенного фильтра, рис.5. Он включает в себя входное R1 и выходное R2 нагрузочные сопротивления, пьезокерамический резонатор горизонтальной ветви П1 и пьезокерамический резонатор вертикальной ветви П2. Предположим, что резонаторы взяты с одинаковой ёмкостью. Пусть резисторы также одинаковы, а по величине равны сопротивлению конденсатора, который имеет такую же ёмкость, как у резонаторов. (Частоту имеем в виду равной номинальной частоте фильтра).
Далее условимся, что мы владеем каким-то фантастическим способом, позволяющим включать и выключать пьезоэффект. Выключив пьезоэффект, мы превратим резонаторы в конденсаторы. Тогда характеристика схемы будет иметь вид пунктирной линии, изображённой на рис.6. Перед тем как включить пьезоэффект раскроем маленькую хитрость. Резонаторы П1 и П2 настроены не на одну и ту же частоту. Их частоты сдвинуты на величину резонансного промежутка Δf таким образом, что резонансная частота fр1 резонатора П1 равна антирезонансной частоте fа2 резонатора П2. Расстановка частот показана на частотной оси рис.6. Рассматривая схему на рис.5 как частотнозависимый делитель напряжения и зная порядки эквивалентных сопротивлений резонаторов П1 и П2 на отмеченных частотах, можно легко убедиться, что частотная зависимость напряжения на выходе делителя будет именно такой, как изображена на рис.6. На этой зависимости имеют место два полюса на частотах fр2 и fа1. В левом полюсе сигнал близок к нулю из-за малого сопротивления резонатора П2, а в правом – благодаря большому сопротивлению резонатора П1. Между полюсами формируется полоса пропускания. Нетрудно видеть, что напряжение на выходе делителя, в точке fа2, fр1, в основном определяется соотношением плеч резистивного делителя R1 и R2. Картина между полюсами радует, чего нельзя сказать о внешней части. Кривая вне полюсов очень быстро сливается с пунктирной линией, где напряжение лишь, приблизительно, в два раза меньше, чем в центре полосы пропускания. Оно, это напряжение, определяется отношением ёмкостей резонаторов. Уменьшив ёмкость резонатора П1 и увеличив ёмкость П2, мы улучшим характеристику фильтра за полюсами. Он будет лучше подавлять сигналы вне полосы пропускания. Повлияет ли такое действие на форму кривой внутри полюсов? Да, повлияет, и в худшую сторону. Но эта форма настолько хороша, что может пойти на некоторые жертвы. Эти жертвы будут незначительны и вполне допустимы при отношении ёмкостей 4 - 6. Поэтому резонаторы для горизонтальных и вертикальных ветвей делают разными. Первые должны иметь ёмкость в несколько раз меньше, чем у вторых, и их выполняют более толстыми и с площадью электрода поменьше. Однако и в этом случае подавление сигнала за пределами полосы пропускания будет недостаточно. Дальнейшее улучшение характеристики фильтров достигается увеличением количества звеньев. Далее познакомимся с устройством промышленного многозвенного лестничного фильтра.
Пьезокерамический фильтр ФП1П1-60
Параметрический ряд фильтров ФП1П1-60 насчитывает более десятка типономиналов. За годы, прошедшие от разработки и начала производства, этих фильтров, в общей сложности, было выпущено около 50 миллионов штук. Такой высокий количественный показатель был достигнут благодаря созданию технологии массового производства резонаторов, простотой его устройства фильтра и лёгкостью сборки.
Фильтр состоит из 7 резонаторов, в том числе 4 резонатора стоят в вертикальных ветвях и 3 резонатора в горизонтальных. При выборе схемы, для обеспечения требуемых характеристик, возможны и другие варианты. Например, 3 резонатора в вертикальных ветвях и 4 – в горизонтальных. Или вариант с 6 или 8 резонаторами (3 или 4 звена). Однако выбранный вариант (см. рис.7а) является уникальным в том смысле, что только он допускает самое простое компоновочное решение при минимальном числе деталей. Это решение иллюстрируется на рис.7б. Только эта принципиальная схема позволила расположить резонаторы в одну линию, чередуясь с одинаковыми пружинящими контактами.
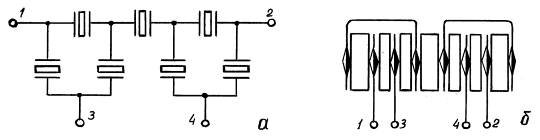
Рис.7. Принципиальная схема пьезокерамического фильтра ФП1П1-60 (а) и соответствующая компоновочная схема (б).
Четыре контакта попарно соединены внутри фильтра, а четыре снабжены внешними выводами. Конструкция фильтра создана на основе этой компоновочной схемы. Фильтр состоит, не считая резонаторов, всего лишь из четырёх видов деталей. Это ячеистый корпус, четыре контакта с выводами, два контакта с перемычками и пластмассовая прокладка для защиты сборки от герметизирующего компаунда. Устройство фильтра и одновременно последовательность сборки, начиная от набора деталей и кончая герметизацией компаундом, показана на рис.8.


Рис.8. Устройство и последовательность сборки пьезокерамического фильтра ФП1П1-60.
Пьезокерамические фильтры ФП1П1-60, имея в своём составе семь резонаторов, обладают превосходными фильтрующими характеристиками и удовлетворяют требованиям подавляющего большинства применений. Лишь в некоторых специальных случаях используются фильтры с увеличенным количеством резонаторов. Рассмотрим типичную амплитудно-частотную характеристику и сделаем некоторые комментарии.
Амплитудно-частотная характеристика
В качестве примера возьмём пьезокерамический фильтр ФП1П1-60-06, который предназначен для формирования частотной характеристики тракта промежуточной частоты сигналов с узкополосной частотной модуляцией. Его типичная амплитудно-частотная характеристика (АЧХ) или, иначе, характеристика затухания приведена на рис.9.
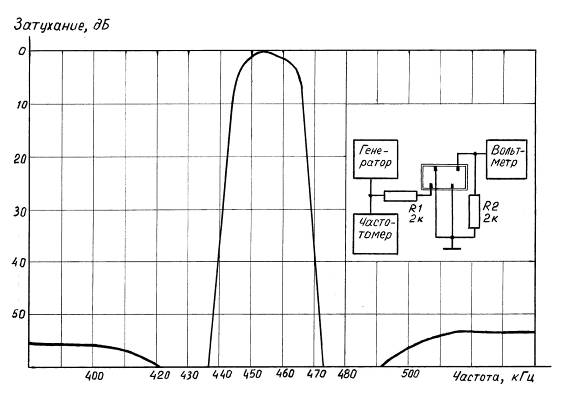
Рис.9. Типичная АЧХ пьезокерамического фильтра ФП1П1-60-06 со схемой измерения.
На поле того же рисунка изображена схема, с помощью которой эта характеристика была снята. Фильтр имеет номинальную частоту 455кГц. Отсчёт затухания ведётся от наивысшей точки АЧХ, в которой фильтр вносит минимальные потери. Минимальная величина вносимого затухания для данного типономинала составляет обычно 2дБ. Характеристика в области полюсов не показана. Она обрезана на уровне 60 дБ. Полосу пропускания оценивают по уровню 6дБ. Она, в этом примере, составляет 21 – 22кГц. Такая полоса необходима для неискажённой передачи сигнала с узкополосной ЧМ. Посмотрим теперь на общие особенности пьезокерамических фильтров в отличие от фильтров, построенных с использованием колебательных LC-контуров, и подробнее обсудим некоторые параметры АЧХ.
АЧХ пьезокерамических лестничных фильтров, будучи составленных из высокодобротных элементов (механическая добротность порядка 500) и имея полюса затухания, отличается очень крутыми склонами. Затухание же, вносимое фильтром в полосе задерживания, постоянно в широком интервале. На очень низких частотах оно увеличивается. На частоте выше номинальной первая паразитная полоса пропускания фильтров с круглыми резонаторами находится вблизи 1,1 – 1,2 МГц. Её относительный уровень составляет 20 – 25дБ от основной полосы. Если фильтр собран из квадратных резонаторов, то паразитная полоса находится около 700кГц. Затухание за пределами полосы пропускания называется гарантированным затуханием. Его нормируют для конкретного диапазона частот, например, fном±100кГц, исключая, конечно, полосу пропускания по уровню заданной величины гарантированного затухания. Задание такой полосы задерживания имеет чисто методический смысл. Так удобно изготовителю осуществлять контроль. Реальная же полоса задерживания начинается от нуля и, фактически, ограничивается первой паразитной полосой пропускания, частота которой была указана выше.
Сделаем несколько замечаний по поводу состава и формулирования параметров АЧХ. Некоторые параметры, в силу традиции, восходящей к LC- фильтрам, применительно к пьезокерамическим фильтрам теряют смысл или превращаются в формальность. Так, важнейшим параметром LC-фильтров является величина затухания при отстройке от центральной частоты. Только этот параметр характеризует его селективность. В случае АМ-сигналов принята отстройка ±9кГц. Это означает, что при ещё большей отстройке затухание будет ещё больше. В случае пьезокерамических фильтров – иная ситуация. Она зависит от того, на какой участок характеристики попадём, отстроившись от центральной частоты. Можно декларировать поистине фантастическое затухание, если величину отстройки совместить с полюсами. Но какой в этом практический смысл, если при ещё большей отстройке затухание быстро уменьшается до величины гарантированного. Существует ряд пьезокерамических фильтров типа ФП1П1-61 (ниже мы вернёмся к ним), типономиналы которых отличаются величиной затухания при отстройке на ±9кГц. Это формальное отличие по существу не сказывается на качестве АМ-тракта, а даёт лишь повод изготовителю назначать более высокую цену за «лучшие» типономиналы. Более естественным для пьезокерамических фильтров и методически более удобным является задание параметров АЧХ в области полосы пропускания путём ограничения снизу полосы пропускания по уровню 6дБ и ограничения сверху по уровню, равному по величине норме гарантированного затухания.
Обсудим форму АЧХ в пределах полосы пропускания. В более простых случаях применения достаточно наложить ограничение на неравномерность характеристики по амплитуде, то есть на относительный уровень всплесков и провалов. Допустим, на характеристике нет всплесков и провалов. Как теперь должна выглядеть идеальная характеристика? Может быть, её вершина должна быть плоская, а склоны строго вертикальными? Оказывается, она не должна быть такой. Любой фильтр вносит в сигнал, помимо амплитудно-частотных, также фазовые искажения. В случае прохождения аналогового сигнала с аудио информацией фазовые искажения значения не имеют, так как сигнал предназначен для наших ушей, которые нечувствительны к фазовым искажениям. Другое дело, когда производится передача сигнала в цифровом формате и сигнал должен затем преобразовываться в аналоговый. В этом случае все компоненты сигнала должны получить одинаковую временную задержку (замедление). Это возможно лишь при линейной фазо-частотной характеристике или параболической амплитудно-частотной характеристике. АЧХ фильтра параболой не может быть в принципе, так как она заключена между асимптотами, однако её центральной части можно придать форму, близкую к параболе.
Пьезокерамические фильтры ФП1П1-61
Возвратимся к рис.7. Отбросим на принципиальной схеме фильтра ФП1П1-60 слева или справа три резонатора, а на компоновочной схеме те же три резонатора и два контакта. Тогда, в конструктивном смысле, будем иметь частный случай более простого фильтра. В фильтре ФП1П1-61 только две детали отличаются от деталей фильтра ФП1П1-60. Это укороченные корпус и прокладка. Фильтры ФП1П1-61, имея уменьшенные размеры и довольно неплохие, благодаря двухзвенной схеме, параметры, нашли самое широкое применение в портативных приёмниках АМ-вещания. Этих фильтров также было выпущено не менее 50 миллионов штук.
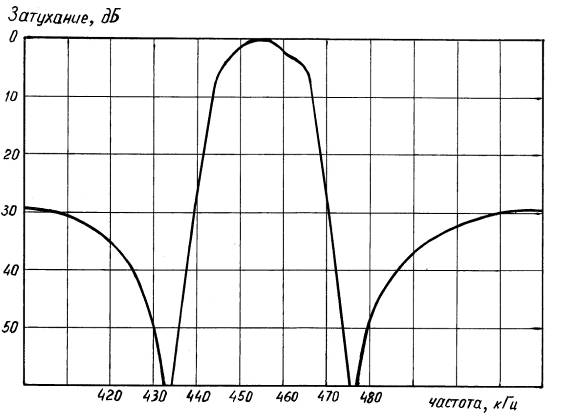
Приведём пример амплитудно-частотной характеристики одного из типономиналов (ФП1П1-61-04) этого фильтра. Она изображена на рис.10. На рис.11 изображены фотографии внешнего вида фильтров ФП1П1-61.
|

|
| Рис.10. Амплитудно-частотная характеристика фильтра ФП1П1-61-04-Х | Рис.11. Фильтры ФП1П1-61 |
Мы выбрали для иллюстрации данный типономинал с тем, чтобы сопоставить с аналогичной по полосе пропускания и номинальной частоте характеристикой фильтра ФП1П1-60-06. Изображение приводим в тех же координатных осях, чтобы показать их отличие в связи с разным количеством резонаторов.
Как управлять параметрами
Это очень просто. Интегральное потребительское качество (назовём это так) дискретного пьезокерамического фильтра определяется количеством резонаторов. Для конкретной принципиальной схемы с выбранным числом резонаторов это качество остаётся постоянным. Имеется в виду следующее. Варьируя параметры резонаторов, можно улучшить тот или иной параметр, но только ценой ухудшения другого параметра. Увеличение ёмкостного отношения влечёт увеличение гарантированного затухания. Это хорошо. Одновременно увеличиваются вносимые потери и уменьшается крутизна склонов. Это плохо. Тем не менее, на практике, этот механизм создания типономиналов используют, так как возможны разные компромиссные решения в зависимости от особенностей применения. Однако основной вопрос, который должен интересовать разработчика – это сколько в фильтре резонаторов. Хорошее гарантирование затухание в полосе задерживания обеспечивается достаточным количеством резонаторов. Фильтр ФП1П1-60 содержит семь резонаторов. Достаточно ли это? Он обеспечивает величину гарантированного затухания не менее 50дБ. Надо ли ещё улучшать этот показатель? Скорей всего нет, потому что затухание свыше 50дБ непросто реализовать в составе устройства без принятия специальных мер по исключению прохождения сигнала в обход фильтра. Монтажная ёмкость между входом и выходом всего в 1пФ уже ограничивает затухание на уровне 40дБ. Для некоторых применений требуются фильтры с особо крутыми склонами АЧХ, например, для выделения одной боковой полосы. В этом случае используют резонаторы с небольшим ёмкостным отношением, а потерю затухания, в связи с этим, восполняют количеством звеньев. Фильтр одной боковой полосы ФП1П1-64 имеет в своём составе 13 резонаторов.
Как управлять шириной полосы пропускания? Ранее мы видели, что расстояние между полюсами фильтра равно удвоенному резонансному (2Δf) промежутку. Ширина полосы пропускания по уровню 6дБ обычно близка к Δf. Она может быть шире или уже. Это зависит от ёмкостного отношения. Резонансный промежуток это показатель полосности. Пьезокерамические материалы, применяемые в фильтрах, покрывают интервал относительных резонансных промежутков (по отношению к номинальной частоте) от 1% до 10%. Стало быть, фильтры на частоту 455кГц могут иметь ширину полосы пропускания по уровню 6дБ от 4-5 до 40-50кГц.
Дискриминаторные фильтры
Основная область применения дискриминаторных фильтров – схемы детектирования частотно-модулированных сигналов. Обычно дискретный дискриминаторный фильтр включает в себя всего лишь один резонатор и представляет собой двухполюсник, а его рабочей характеристикой служит фазо-частотная характеристика.
Прохождение сигнала в устройстве детектирования с применением пьезокерамического дискриминаторного фильтра происходит следующим образом. Ограниченный по амплитуде частотно-модулированный сигнал поступает на элемент фильтра, на выходе которого приобретает фазовый сдвиг, пропорциональный отклонению частоты сигнала от несущей частоты. Сигнал приобретает фазовую модуляцию по закону частотной. Затем фазо-модулированный сигнал поступает на фазовый детектор. На второй вход фазового детектора поступает, в качестве опорного, тот же сигнал, но без приобретённого фазового сдвига. На выходе фазового детектора выделяется демодулированный низкочастотный сигнал. Напряжение демодулированного сигнала пропорционально приобретённому фазовому сдвигу. Чтобы после демодуляции сигнал получился без искажений, приобретённый фазовый сдвиг также должен быть пропорционален отклонению частоты. А это значит, что фазо-частотная характеристика фильтра должна быть линейна в рабочем интервале частот.
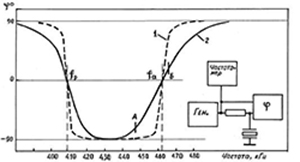
Резонатор полосового фильтра, нельзя использовать как элемент дискриминаторного фильтра. На его фазо-частотной характеристике нет подходящего рабочего участка. Она состоит, либо из слишком пологих, либо из слишком крутых участков. Причина тому – высокая добротность. Для дискриминаторных фильтров применяется пьезокерамика с пониженной (50 – 100) механической добротностью. На рис.12 приведены фазо-частотные характеристики пьезокерамических резонаторов.
|

|
| Рис.12. Фазо-частотные характеристики пьезокерамических резонаторов с высокой механической добротностью (кривая 1)и с пониженной добротностью (кривая 2) | Рис.13. Пьезокерамический дискриминаторный фильтр ФП1Д1-22 |
В условиях серийного производства фазо-частотную характеристику дискриминаторных фильтров контролирует опосредованно. Непосредственно измеряются параметры демодулированного сигнала – амплитуда сигнала и коэффициент нелинейных искажений. Более того, нормы на эти параметры устанавливают для конкретной схемы детектирования, в составе которой контролируют фильтр, и при оговоренной величине девиации несущей. Существует множество интегральных микросхем приёмных трактов, которые предназначены для работы с пьезокерамическими дискриминаторными фильтрами. Каждый тип микросхемы по-своему влияет на фазо-частотную характеристику фильтра. Микросхемы также отличаются по степени предварительного усиления демодулированного сигнала. Поэтому нормы на параметры дискриминаторных фильтров формулируют применительно к «своей» микросхеме. В частности, фильтры ФП1Д1-22 были разработаны для использованя в паре с микросхемой К174ХА26 или с её аналогами.
